| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 백준 16236
- 웹어플리케이션 서버
- Coroutine
- Spring Boot
- spring cloud
- 백준 16719
- Spring
- springboot
- Kotlin
- java 기술면접
- spring oauth
- 백준 15685
- 백준 16235
- 백준
- spring security
- MSA
- with recursive
- 파이썬
- 백준 17626
- 백준 19238
- JVM
- MySQL
- 백준 파이썬
- 프로래머스
- re.split
- 백준 17779
- sql 기술면접
- JPA
- java
- 프로그래머스
- Today
- Total
시작이 반
다익스트라(Dijkstra) 본문
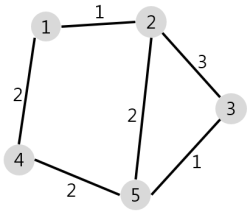
필요 항목
PriorityQueue
graph[][]
dist[]
ex) 양방향
Vertex = n
Edge[][] = [[1, 2, 1], [2, 3, 3], [5, 2, 2], [1, 4, 2], [5, 3, 1], [5, 4, 2]]
(u, v, cost)
다익스트라는 2차원 배열을 선언하여 graph[u][v] = cost 를 저장한다.
(벨만포드는 edge(u, v, cost)만 보고 2중 반복문)
int[][] graph = new int[n][n];
양방향이기 때문에 graph[u][v] 와 graph[v][u] 를 둘다 채워준다.
for( int[] edge... Edge ){
int u = edge[0];
int v = edge[1];
int cost = edge[2];
graph[u][v] = cost;
graph[v][u] = cost;
}
dist = 해당 지점까지 거리
PriorityQueue.add(new int[]{해당 지점, dist[해당지점]})
Dijkstra(graph[][], dist[], priorityQueue, start){
dist[start] = 0;
priorityQueue.add(new int[]{start, dist[start]});
while(!priorityQueue.isEmpty()){
int[] pop = priorityQueue.remove();
int now = pop[0];
for( i = 0 ... vertex개수 ){
if( graph[now][i] != 0 ){
if( dist[i] > dist[now] + graph[now][i] ) {
dist[i] = dist[now] + graph[now][i];
priorityQueue.add(new int[]{i, dist[i]});
}
}
}
}
}
'알고리즘 > 활용 방법' 카테고리의 다른 글
| 벨만-포드 (Bellman-Ford) (0) | 2021.09.15 |
|---|---|
| 백트래킹(Backtracking) (0) | 2021.01.09 |
| DFS/BFS 활용 문제 (0) | 2021.01.06 |


